1. The "30" degree triangle at first has the shortest leg labeled "x", the longer leg labeled "x radical 3", and the hypotenuse labeled as 2x. To simplify the three sides of this triangle so that the hypotenuse=1, I divided all the sides by two. I would then have, in order from shortest to longest side: x/2, (x radical 3)/2, and x. Finally, the last step is to label the ordered pairs. Since the triangle is drawn in the 1st quadrant, all values will be positive. The point at the 30 degrees is the origin, which is (0,0). The point at the 90 degrees, or the square angle, is (radical 3 over 2, 0). This is because we go over (radical 3)/2 units for the x value, while the y value stays the same as 0 since we do not go up or down. Lastly, the point at the 60 degrees will be (radical 3 over 2, 1/2). It has the same x value as the previous ordered pair, but since it goes up 1/2 units, that will become our y value.
2. The "45" degree triangle at first has its two congruent legs labeled as "x", while the hypotenuse is labeled as "x radical 2". To simplify the three sides of this triangle so that the hypotenuse=1, I divided all the sides by radical 2 to cancel out the one on the hypotenuse. I would then have, from the two shortest to the hypotenuse: x/(radical 2), x/(radical 2), and x. Since I cannot have a radical on the bottom of the fraction, I rationalize the two legs by multiplying both the top and bottom of the fraction by radical 2. I would then be left with (x radical 2)/2, (x radical 2)/2, and x. Finally, the last step is to label the ordered pairs. Since the triangle is drawn in the 1st quadrant, all values will be positive. The point at the first 45 degrees is the origin, which is (0,0). The point at the 90 degrees, or the square angle, is (radical 2 over 2, 0). This is because we go over (radical 2)/2 units for the x value, while the y value stays the same as 0 since we do not go up or down. Lastly, the point at the second 45 degrees will be (radical 2 over 2, radical 2 over 2). It has the same x value as the previous ordered pair, but since it goes up (radical 2)/2 units, that will become our y value for this ordered pair.
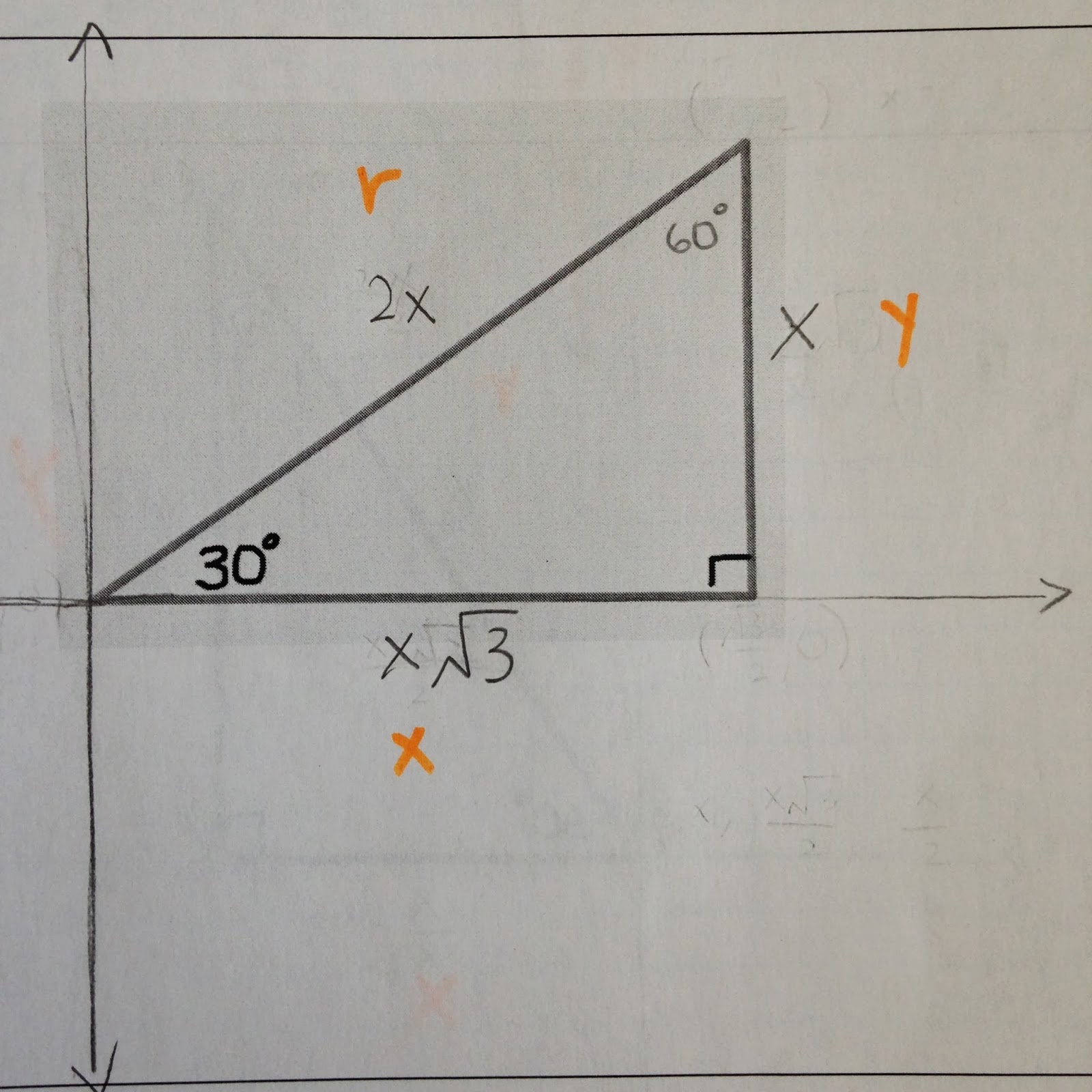
3. The "60" degree triangle at first has the shortest leg (which is now horizontal) labeled x, the longer leg (which is now vertical) labeled as x radical 3, and the hypotenuse labeled as 2x. To simplify the three sides of this triangle so that the hypotenuse=1, I divided all the sides by 2. I would then have, in order from shortest to longest side: x/2, (x radical 3)/2, and x. Finally, the last step is to label the ordered pairs. Since the triangle is drawn in the 1st quadrant, all values will be positive. The point at the 60 degrees is the origin, which is the ordered pair (0,0). The point at the 90 degrees, or the square angle, is (1/2, 0). This is because we go over 1/2 units for the x value, while the y value stays the same as 0 since we do not go up or down. Lastly, the point at the 30 degrees will be (1/2, radical 3 over 2). It has the same x value as the previous ordered pair, but since it goes up (radical 3)/2 units, that will become our y value.
4. The activity helps derive the unit circle by giving us a much better understanding of it as a whole. We can visualize the special right triangles within the unit circle, realizing that their ordered pairs of the hypotenuse and opposite side will create a part of the circle. We will know where the points had come from, along with their corresponding degrees, due to the special right triangles, and we will realize that the unit circle is entirely made up of those triangles and apply that to our previous knowledge about them.
5. The triangles of this activity lie in the first quadrant, where both x and y are positive. However, the positive values of the ordered pairs will change if you draw them in different quadrants--x will be negative in the second quadrant, y will be negative in the fourth quadrant, and both x and y will be negative in the third quadrant. These will apply to the ordered pairs of the triangles. For example, the 45 degree triangle is drawn in the 2nd quadrant. Therefore, the x of its ordered pair will be negative. The 30 degree triangle is drawn in the 3rd quadrant. Both its x and y will be negative in the ordered pair. Finally, the 60 degree triangle is drawn in the 4th quadrant, so only the y value of the ordered pair is negative.
Inquiry Activity Reflection
The coolest thing I learned from this activity was that all of the special right triangles drawn in the first quadrant of a coordinate plane (starting at the origin) and their reference angles drawn in all the other coordinate planes make up the unit circle! All you have to do is connect the points to form a circle. I understood how to unit circle was formed and now it is easier to memorize it as a whole.
This activity will help me in this unit because I now I have a full understanding of where the unit circle comes from. It helps me in memorizing the unit circle and applying it to later concepts, such as 8 and 9. I know how the ordered pairs on the unit circle were derived and their corresponding degrees as well.
Something I never realized before about special right triangles and the unit circle is that they are both connected! I learned that one can derive the unit circle from special right triangles by using the 45 45 90 and 30 60 90 triangles. I like how trigonometry is built on concepts we studied in geometry. It was really interesting to see how the special right triangles applied to the unit circle and it helped tremendously in memorizing it for me.








.JPG)