Continuity is when a graph has no breaks, no jumps, and no holes. It is predictable, and you are able to draw it without lifting your pencil from the paper. For a graph to be continuous at a certain point, it must be approaching the same left and right to an existing value and the limit and the value must be the same. On the other hand, a discontinuity is when the graph has a break, jump, or hole. It is the exact opposite of a continuous graph.
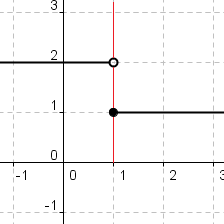
There are four type of discontinuities: point, jump, oscillating, infinite. The point discontinuity falls into the removable discontinuity category. It is essentially an open hole in the graph, and it may or may not have a value at a different height. This discontinuity is shown in the top left picture below. The following three discontinuities are classified as non-removable. The jump discontinuity, as shown on the top middle picture below, is when the graph "jumps" from one point to another, approaching a different point from the left and the right. The two points where the graph jumps can be open and closed or both open, but it can never be both closed. A third type of discontinuity is oscillating behavior, shown on the top right picture below. This is when the graph becomes extremely wiggly, going up and down in a random and unpredictable fashion. Finally, the last type of discontinuity is an infinite discontinuity, which is shown in the bottom picture below. This exists when there is a vertical asymptote and leads to unbounded behavior, where the graph approaches infinity and negative infinity on the side.
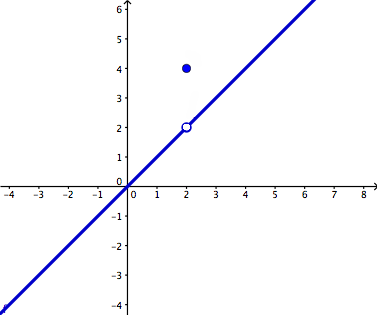


2. What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?
A limit is the intended height of a function, meaning the height that the graph is looking like it is going to reach at a certain point. It exists when the graph is continuous or when there is a point discontinuity (the removable discontinuity). In other words, the graph has a limit when it is approaching the same left and right on both sides, does not have unbounded behavior or a vertical asymptote, and does not have oscillating behavior as well.
Similarly, a limit does not exist during the three non-removable discontinuities: jump, oscillating, and infinite. There is no limit at a jump discontinuity because the graph is approaching different points from the left and right. There is no limit at oscillating behavior because it is random and unpredictable, and we cannot determine the intended height. Finally, there is no limit at an infinite discontinuity because the graph has unbounded behavior due to the vertical asymptote.
The difference between a limit and a value is that the limit is the intended height of the function. On the other hand, a value is the actual height of the function. When a graph is continuous, the limit and the value is the same--in other words, the intended height and the actual height are at the same point, which means that the graph is going where it is supposed to.
3. How do we evaluate limits numerically, graphically, and algebraically?
We evaluate limits numerically on a table, where we can visualize the numbers we will use. First, we set it up and put the number that x is approaching in the middle of the x row. On the sides of that number, add values that get increasingly closer to it--for example, if x is approaching 3, put values like 2.9 on the left and 3.1 on the right. Then, plug the function into a calculator, trace the x values that you have chosen, and then fill in the rest of the table (which should just be the y row). Determine what the y values seem to be getting closer to, and that will be your limit.
Next, we evaluate limits graphically by looking at a graph. We put our fingers to the left and right of the point that the problem wants us to find the limit for. If our fingers travel along the graph and meet, then the limit exists at that point. However, if our fingers travel along the graph and do not meet or end up at separate points, the limit does not exist. This means that there is a non-removable discontinuity present.
Finally, we evaluate limits algebraically three ways: direct substitution, dividing out, and rationalizing/the conjugate method. The direct substitution method is simple--all you have to do is to plug in the number that x is approaching into the equation and then solve. However, if you end up with an indeterminate answer, 0/0, then that means that you have to use one of the other two methods: dividing out or rationalizing/conjugate method. Always use direct substitution first before resorting to these two methods. The dividing out or factoring method involves factoring out either the numerator or the denominator to see if anything cancels. This way, we can plug x back into the function after we have cancelled out something so that we don't get another indeterminate answer. The last method is the rationalizing or conjugate method. This is when you multiply the fraction by the conjugate of either the numerator or the denominator. You leave the non-conjugate denominator/numerator factored, and something well cancel out on the top and bottom. After doing this, you will be able to use direct substitution and plug back in x, solving the problem.