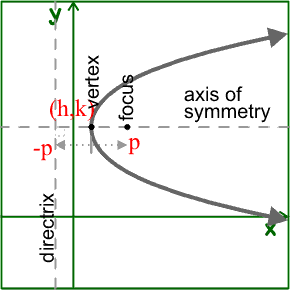
2. Description of a parabola: The formula or equation for a parabola is (x-h)^2=4p(y-k) or (y-k)^2=4p(x-h). On a graph, a parabola resembles something similar to a curve, forming an arch-like shape when graphed, and is symmetrical on both sides of its vertex. One of the key features of a parabola is the vertex. It is defined as the point where the parabola crosses its axis, and can be identified using (h,k) of the equation or finding the point that is on the axis of symmetry that "divides" the parabola. Another key feature of the parabola is the aforementioned axis of symmetry. This is the line that the vertex lies on and is what splits the parabola into two symmetrical sides, each mirroring each other. It is either vertical or horizontal, depending on whether the parabola is going up and down or left and right. As a result, the equation of the axis of symmetry will start with x= or y=.
To continue with, there are many other key features to the parabola that are introduced in this unit. One of them is the focus, which lies on the axis of symmetry along with the vertex. The focus will always be "inside" of the parabola, meaning that the parabola will be opening towards it. The closer it is to the vertex, the "skinnier" the graph will be, and the farther away the focus is from the vertex, the "fatter" the graph will be. Since the focus is relatively closer to the vertex, as seen in the picture, the parabola is more skinny that it is fat. The focus point is "p" units away from the vertex, a number that can be determined by referencing the formula of the parabola. The variable "p" can also determine which way the parabola is opening up to--for example if p is positive, the graph will open up or right, while if p is negative, the graph will open down or left. To refer to the picture below once again, the graph is opening right, which tells us that "p" was a positive number. In addition, the same distance p is from the vertex is counted in the opposite direction to determine the directrix, which is a line that is perpendicular to the axis of symmetry.
 |
| https://people.richland.edu/james/lecture/m116/conics/translate.html |
3. Real World Application: A real world application for the parabola can be seen in the headlights of many automobiles, which are in the shape of paraboloids and help focus light into a certain beam. In other words, the shape of the headlights is concave, allowing more light to be beamed from it. This is because the light is directed to the focus of the parabolic mirror as it travels, then is immediately reflected in straight lines that are parallel to the axis of symmetry. The headlight has a smooth inner surface of a glass reflector, which in turn has a layer of bright aluminum. This part of the object serves as a powerful reflector. As a result, this is what makes the beam of headlights and similar objects to be incredibly strong, projecting light with a wider distance and range. It gives off an intense concentrated beam of light.
The light is also beamed in many directions to encourage safer night driving. Therefore, designers do not want all of the light beams to be parallel to the axis of symmetry--some of the light has to be aimed in different places. To do this, they "offset the filament from the focus and change [the direction of] the beam entirely" (http://www.pleacher.com/mp/mlessons/calculus/appparab.html). The positions that the filaments are in are a major factor in determining the different illumination patters that have been desired. For example, if the filament is directed above the focal point, or the focus, the rays of light will be reflected downward. Similarly, if the filament is directed below the focal point, the rays of light will be reflected upward. And if the filament is positioned behind the focal point, then the rays of light will converge. A video explaining this concept further along with other uses of parabolas in real life is embedded below.
4. Works Cited:
- http://www.pleacher.com/mp/mlessons/calculus/appparab.html
- http://www3.ul.ie/~rynnet/swconics/UP.htm
- https://people.richland.edu/james/lecture/m116/conics/translate.html
No comments:
Post a Comment