BQ7: Unit V

Explain in detail where the formula for the difference quotient comes from.
The difference formula is essentially the formula for the slope of a line--more specifically, the secant of another graph. Because of this, we can relate it to the original slope formula, which is (y2-y1)/(x2-x1). Our first step for deriving the difference formula is to find the coordinates of a line that we can apply it to. The graph drawn below illustrates a line and two points on it, which are (x, f(x)) and (x+h, f(x+h)). We use h because it represents the change in x from one point on the x or y axis to another. This is why h is also sometimes known as delta x.

We want to find the slope of this line, so we plug in the two coordinates into the slope formula. After doing this, we are left with: f(x+h)-f(x) over (x+h)-x. This is already looking like the different quotient we know of, and after this we only have to do a little bit of simplifying. The positive x and the negative x will cancel each other out, and so our final answer would be: f(x+h)-f(x)/h. This is how we would derive the difference quotient from the slope formula.

BQ 6: Unit U Concepts 1-8

1. What is continuity? What is discontinuity?
Continuity is when a graph has no breaks, no jumps, and no holes. It is predictable, and you are able to draw it without lifting your pencil from the paper. For a graph to be continuous at a certain point, it must be approaching the same left and right to an existing value and the limit and the value must be the same. On the other hand, a discontinuity is when the graph has a break, jump, or hole. It is the exact opposite of a continuous graph.
There are four type of discontinuities: point, jump, oscillating, infinite. The point discontinuity falls into the removable discontinuity category. It is essentially an open hole in the graph, and it may or may not have a value at a different height. This discontinuity is shown in the top left picture below. The following three discontinuities are classified as non-removable. The jump discontinuity, as shown on the top middle picture below, is when the graph "jumps" from one point to another, approaching a different point from the left and the right. The two points where the graph jumps can be open and closed or both open, but it can never be both closed. A third type of discontinuity is oscillating behavior, shown on the top right picture below. This is when the graph becomes extremely wiggly, going up and down in a random and unpredictable fashion. Finally, the last type of discontinuity is an infinite discontinuity, which is shown in the bottom picture below. This exists when there is a vertical asymptote and leads to unbounded behavior, where the graph approaches infinity and negative infinity on the side.


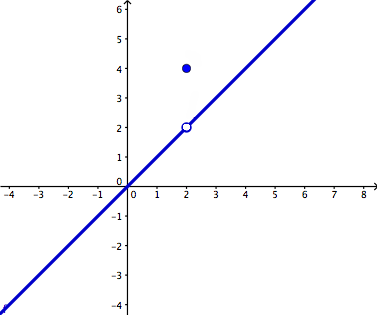
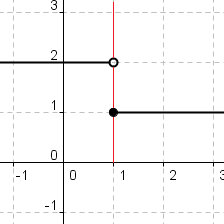
2. What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?
A limit is the intended height of a function, meaning the height that the graph is looking like it is going to reach at a certain point. It exists when the graph is continuous or when there is a point discontinuity (the removable discontinuity). In other words, the graph has a limit when it is approaching the same left and right on both sides, does not have unbounded behavior or a vertical asymptote, and does not have oscillating behavior as well.
Similarly, a limit does not exist during the three non-removable discontinuities: jump, oscillating, and infinite. There is no limit at a jump discontinuity because the graph is approaching different points from the left and right. There is no limit at oscillating behavior because it is random and unpredictable, and we cannot determine the intended height. Finally, there is no limit at an infinite discontinuity because the graph has unbounded behavior due to the vertical asymptote.
The difference between a limit and a value is that the limit is the intended height of the function. On the other hand, a value is the actual height of the function. When a graph is continuous, the limit and the value is the same--in other words, the intended height and the actual height are at the same point, which means that the graph is going where it is supposed to.

3. How do we evaluate limits numerically, graphically, and algebraically?
We evaluate limits numerically on a table, where we can visualize the numbers we will use. First, we set it up and put the number that x is approaching in the middle of the x row. On the sides of that number, add values that get increasingly closer to it--for example, if x is approaching 3, put values like 2.9 on the left and 3.1 on the right. Then, plug the function into a calculator, trace the x values that you have chosen, and then fill in the rest of the table (which should just be the y row). Determine what the y values seem to be getting closer to, and that will be your limit.
Next, we evaluate limits graphically by looking at a graph. We put our fingers to the left and right of the point that the problem wants us to find the limit for. If our fingers travel along the graph and meet, then the limit exists at that point. However, if our fingers travel along the graph and do not meet or end up at separate points, the limit does not exist. This means that there is a non-removable discontinuity present.
Finally, we evaluate limits algebraically three ways: direct substitution, dividing out, and rationalizing/the conjugate method. The direct substitution method is simple--all you have to do is to plug in the number that x is approaching into the equation and then solve. However, if you end up with an indeterminate answer, 0/0, then that means that you have to use one of the other two methods: dividing out or rationalizing/conjugate method. Always use direct substitution first before resorting to these two methods. The dividing out or factoring method involves factoring out either the numerator or the denominator to see if anything cancels. This way, we can plug x back into the function after we have cancelled out something so that we don't get another indeterminate answer. The last method is the rationalizing or conjugate method. This is when you multiply the fraction by the conjugate of either the numerator or the denominator. You leave the non-conjugate denominator/numerator factored, and something well cancel out on the top and bottom. After doing this, you will be able to use direct substitution and plug back in x, solving the problem.

BQ #3: Unit T Concepts 1-3

How do the graphs of sine and cosine relate to each other the others? Emphasize asymptotes in your response.

a. Tangent? The graph of tangent has its asymptotes based on cosine. To understand how this works, one must know that asymptotes are found in a graph when the trigonometric function is undefined. The trig ratio for tangent is sine/cosine, and we know that it is undefined when the denominator is equal to zero. So, if cos(x)=0, tangent becomes undefined, and thus it has asymptotes. Cosine equals zero at pi/2 and 3pi/2, so we know that two of our asymptotes lie there. Also, the positive and negative values of tangent are influenced by sine and cosine. For example, in quadrant two, sine is positive while cosine is negative. When we divide sine by cosine, since it is tangent's ratio, we get a negative value. Thus, we find that tangent is negative in quadrant two, which is true. This method applies for each quadrant around the unit circle.

b. Cotangent? The graph of cotangent has its asymptotes based on sine. The trig ratio for cotangent is cosine/sine, and we know that it is undefined when the denominator is equal to zero (thus giving us asymptotes). So, if sine(x)=0, cotangent becomes undefined, and then it has asymptotes. Sine equals zero at 0 and pi, so we know that two of our asymptotes lie there. Also, the positive and negative values of cotangent are influenced by sine and cosine because of its ratio. For example, in quadrant three, both sine and cosine are positive. When we divide cosine by sine, since it is cotangent's ratio, we get a positive value (a negative divided by a negative equals a positive). Thus, we find that cotangent is positive in quadrant three, which turns out to be true. This method applies for each quadrant around the unit circle.

c. Secant? The graph of secant has its asymptotes based on cosine, since it is its reciprocal. The trig ratio for secant is 1/cosine, and we know that it becomes undefined when the denominator is equal to zero (thus giving us asymptotes). So, if cosine(x)=0, secant becomes undefined, and then it has its asymptotes. Cosine equals zero at pi/2 and 3pi/2, so we know that two of our asymptotes lie there. Also, the positive and negative values of secant are also influenced by cosine, since they share the same ones.

d. Cosecant? The graph of cosecant has its asymptotes based on sine, since it is its reciprocal. The trig ratio for cosecant is 1/sine, and we know that it becomes undefined when the denominator is equal to zero (thus giving us asymptotes). So, if sine(x)=0, cosecant becomes undefined, and there we have our asymptotes. Sine equals zero at 0 and pi, so we know that we have two of our asymptotes there. Also, the positive and negative values of secant are also influenced by sine, since they share the same ones.

BQ 4: Unit T Concept 3

Why is a "normal" tangent graph uphill, but a "normal" cotangent graph downhill? Use unit circle ratios to explain.
The tangent graph is uphill while the cotangent graph is downhill due to their asymptotes, and this is because of their different trig ratios. Tangent's is y/x, while cotangent's is x/y. As we have learned in the previous concepts, asymptotes exist where the trig function of the graph is undefined, or when its denominator is equal to zero. Therefore, tangent would be undefined whenever x=0 (pi/2 and 3pi/2), while cotangent would be undefined whenever y=0 (0 and pi).

Even though the signs may be the same for the two graphs--positive-positive-negative-negative--tangent and cotangent graphs are different because their asymptotes are in different places. Thus, their whole graphs are "shifted" and this results in tangent going uphill and cotangent going downhill according to the signs.

BQ #5: Unit T Concepts 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.
Asymptotes appear on graphs where the values are undefined, or when a ratio is divided by zero. The reason that the sine and cosine graphs do not have any asymptotes is because, according to their unit circle ratios, none of their values will ever turn out undefined. For example, y/r and x/r are the sine and cosine ratios, respectively, and we know that r always equals one. Thus, these ratios cannot possibly be divided by zero, so they will never be undefined.

However, the cosecant, secant, tangent and cotangent graphs will have asymptotes. This is because their ratios have either x or y as denominators, and there is a possibility of a denominator of zero. Secant and tangent are undefined at pi/2 or 3pi/2 (when x=0), and cotangent and cosecant are undefined at 0 and pi (when y=0).

BQ #2: Unit T Concept Intro

How do the trig graphs relate to the Unit Circle?

1. Period? - Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi? The period for sine and cosine 2pi because, going around the Unit Circle, their patterns take the whole circle to repeat again. For example, sine's pattern is positive positive negative negative. Since there is no clear pattern, we must use the whole Unit Circle to repeat it again and thus, the period is 2pi. The same can be applied to cosine's pattern around the Unit Circle, which is positive negative negative positive. Similarly, it has to be repeated again for a pattern to emerge, so the period for cosine is 2pi (the distance around the Unit Circle). 

Tangent and cotangent, on the other hand, have a clear repeating pattern without having to go all the way around the Unit Circle: positive negative positive negative. We see that "positive, negative" is the repeating pattern and that it repeats itself halfway around the Unit Circle. Then, it starts over again. As a result, the period of tangent and cotangent is only pi, which is half the distance around the Unit Circle.

2. Amplitude? - How does the fact that sine and cosine have amplitudes of one (and the other trig functions don't have amplitudes) relate to what we know about the Unit Circle? Sine and cosine having amplitudes of one relates to the Unit Circle in an important way. First of all, to understand the amplitudes of sine and cosine, we would have to know that the range of the Unit Circle values. They are between 1 and negative 1. And so, with sine having a ratio of y/r--or simply 'y'--the graph's amplitude is limited to one. Thus, the amplitude will remain at one. Cosine, similarly, has a ratio of x/r--or simply 'x', since r is 1--and its graph will have an amplitude of 1.

Reflection #1: Unit Q: Verifying Trig Identities

1. What does it actually mean to verify a trig identity?
To verify a trig identity means to confirm that both sides of the equation are equal to one another, or that the equation is true. We do this by using different identities that we need to prove the equations that we are given.

2. What tips and tricks have you found helpful?
I have found that converting every trig function to sine and cosine helps when verifying or simplifying. Other tricks that I have found helpful is to split fractions that have monomial denominators to simplify even further or to combine fractions with a binomial denominator. It also helps me to look for greatest common factors to factor out of polynomials in the equation and then possibly use Pythagorean identities to simplify.

3. Explain your thought process and steps you take in verifying a trig identity.  Do not use a specific example, but speak in general terms of what you would do no matter what they give you.
My first step is look for any trig functions that can be converted into sine and cosine, as those are the easiest to work with. If the trig functions are squared in the equation, I would also look for the trigonometric pairs that go with each other: sine and cosine, cosecant and cotangent, and tangent and secant. If I have those, then I would use them instead of converting. I might change one of the trig functions to the other using a Pythagorean identity. However, if I do not have any trig functions squared, then converting everything to sine and cosine is the simplest way.

If I have a fraction, I will look for two things. One of them is if I can multiply the numerator and denominator by the denominator's conjugate. This will work only if I have a binomial denominator and if I can't cancel anything out on the top and bottom anymore. After I multiply in the conjugate, I most likely will end up with a Pythagorean identity, so I can substitute in one trig function and split the fraction if I have to--only if I cannot simplify the numerator and denominator of the fraction first.

SP #7: Unit Q Concept 2: Finding All Trig Functions When Given One Trig Function and Quadrant (Using Identities)

Given this problem:

Find the missing trig functions.

Using Identities

Using SOHCAHTOA
The first thing that you need to do for this problem is find the hypotenuse. Do this by using the Pythagorean Theorem. You should get rad34. 
We know that:
Tanx= -5/3
Secx= -\|34/3

If tan & sec are negative the. We know we are in the 2nd quadrant. To find sin, cos, csc, cot, we use the ratios. Go back to unit N if you need to review the ratios. If you need help look at the picture for reference.

A viewer needs to pay special attention to the two different methods of solving these trigonometric functions. Even though it uses both identities and the old SOHCAHTOA method, the answers still turn out the same. This shows that one can use either identities or SOHCAHTOA to solve for different trig functions, because they both work for the same problem.

This SP was made in collaboration with Bryan Arciniega.

I/D3: Unit Q - Pythagorean Identities

Inquiry Activity Summary:
1. Where does sin^2x+cos^2x=1 come from?
This identity is derived from the Pythagorean theorem, and that is why it is known as a Pythagorean identity. Drawing from our knowledge about the unit circle, the Pythagorean theorem using x, y, and r would be: x^2+y^2=r^2. From here, we would perform an operation that makes the Pythagorean Theorem equal to 1, which is part of the identity. This would then result in: (x/r)^2+(y/r)^2=1. A pattern that we notice is that the unit circle trig ratio for cosine is x/r, while the unit circle trig ratio for sine is y/r. As a result, we can plug these two trig functions into our equation, and thus we derive the Pythagorean identity.
2. Show and explain how to derive the two remaining Pythagorean identities from sin^2x+cos^2x=1.
To derive the two remaining Pythagorean identities, we can perform similar operations:

• For the first derivation, we divide the equation by cos^2x. This will leave us with several functions that can be converted using trig identities. Cos^2x/cos^2x cancels out as 1, sin^2x/cos^2x is equivalent to tan^2x (as seen in a ratio identity), and 1/cos^2x is equivalent to sec^2x (as seen in a reciprocal identity). This leaves us with 1+tan^2x=sec^2x.

• For the second derivation, we divide the equation this time by sin^2x. This will leave us with several functions that can be converted using trig identities. Cos^2x/sin^2 is equivalent to cot^2x (as seen in a ratio identity), Sin^2x/sin^2x cancels out as 1, and 1/sin^2x is equivalent to csc^2x (as seen in a reciprocal identity). This leaves us with cot^2x+1=csc^2x.

Inquiry Activity Reflection:
The connections that I see between Units N, O, P, and Q so far are that they all deal with triangles and angles in some way. We are learning how to solve different kinds of triangles, from right triangles to acute and obtuse ones that we needed to apply the Law of Sines and Cosines to. We are using the trigonometric functions derived from triangles (sin, cos, tan, etc.) and using them as identities or to find angles in the unit circle. Another connection that can be seen between these four units is that most of them deal with the unit circle--for example, we just derived the Pythagorean identities using trig functions from the unit circle and can prove them using points from it.
If I had to describe trigonometry in three words, they would be complicated, challenging, and rewarding to learn. It is complicated because there are many derivations that we must learn and, more importantly, understand if we want to grasp a concept. Everything that we learn is built on something else, and it is important to understand these things before we move on to something new. Also, trigonometry is challenging because there are many formulas, many identities to memorize in order to succeed. Memorization is the biggest and most challenging part, because once we know the material well, we will be able to do well on the tests. Finally, trigonometry is almost rewarding to learn because I enjoy the feeling of success that comes after solving a triangle or simplifying a trig function using identities. It may be difficult at first, but once I know the concepts well, I am very satisfied with learning them.

WPP 13-14: Unit P Concepts 6-7: Application of the Law of Sines and the Law of Cosines

The Ultimate Crossover Finale: Part 1

http://25.media.tumblr.com/5927df0165a2a3c16b1299503df2d3be/tumblr_mhb0d5qkFy1rmt8bgo1_500.jpg

Bryan and Sarah are on the same team when playing capture the flag. However, whoever gets to the enemy's flag first will win all the glory for their team. They are 47 yards apart on an east-west line. Between them in the distance, they see the enemy's flag mounted on a pedestal. Bryan's bearing to the flag is N 23 degrees E, while Sarah's bearing to the flag is N 36 degrees W. Find each person's distance from the flag. Who is closer? (Round your answers to the nearest hundreth.)

The Ultimate Crossover Finale: Part 2

http://designlap.com/eye-catching-beach-wallpapers/

Bryan and Sarah are now working as lifeguards. Bryan and Sarah's life guard post are 550 feet apart. Sarah spots a person in need at 213°. Being a great mathematician, Sarah calculates she is 700 feet away from this person. How far is Bryan from the person in need?                                         This WPP was made in collaboration with Bryan Arciniega.

BQ# 1: Unit P Concepts 1-5

1. Law of Sines: The law of sines is important in finding the values for non-right triangles. By setting up a proportion, one can find the value of a side or an angle in a triangle if we have all the necessary information. The law of sines works best when we have an angle-angle-side, angle-side-angle, or even an side-side-angle triangle.

5. Area Formulas: All three formulas to find the area of the triangle--the "traditional" formula, area of an oblique triangle, and Heron's formula--will result in the same value: 4.2 units squared.

WPP 12: Unit O Concept 10: Finding Angles of Elevation and Depression

http://www.timeanddate.com/holidays/un/international-mountain-day

a) Percy is going on a hike with his friends up a mountain. His friend, Annabeth (who is a total genius), measures that the angle of elevation to the top of the mountain to be 72 degrees. Assuming that she, Percy, and their group of friends are standing 205 feet away from the base of the mountain, how tall is the mountain? (Round to the nearest foot)

b) Percy and his friends reach the peak of the mountain a few hours later. They are going to hike down to a lodge at the base of the mountain from the other side, which is less steep. It has an angle of depression of 41 degrees. Since they are ____ ft high up on the mountain, how long is the trail they will hike this time?

Solution:

I/D1: Unit O - Derive the Special Right Triangles

Inquiry Activity Summary
1. To derive the 30-60-90 triangle from a equilateral triangle with all side lengths of 1, we first have to cut the triangle in half down the middle, perpendicular to the base side. The angles that will have been formed in the new triangle (either half of the divide) are 30, 60, and 90 degrees. The 90 degrees is formed from the perpendicular cut and the base of the triangle, the 60 degrees is the untouched angle of the new triangle, while the 30 degrees angle has been the angle cut in half where the divide had begun at (half of 60 degrees is 30 degrees).
For the side lengths, the hypotenuse is still one, since that was the original length of a side of the equilateral triangle. The 30 degree side is 1/2, since the triangle had been cut in half from the base and we are deriving half of the original side length of 1. Finally, the 60 degree side can be derived using the Pythagorean theorem. We must solve for 'b' once we plug in the numbers for 'a' and 'c' (1/2 and 1, respectively, corresponding to their angles). When we simplify and get the 'b' variable on its own, b^2 will be equal to 3/4. As a result, the value of b would be radical 3 over 2. Finally, we must multiply all the side lengths by 2 to simplify them, since we do not want fractions. The new side lengths would be, in ascending order: 1, radical 3, and 2. The last step is to substitute the values with the 'n' variable where n=1. This shows that these values can be applied to any multiples of themselves. Now, the new side lengths would be, in ascending order, 'n' to the 30 degree side, n radical 3 to the 60 degree side, and 2n to the 90 degree side.

2. To derive the 45-45-90 triangle from a square with all side lengths of 1, we first have to cut the square in half diagonally, from one corner to another. The angles that will have been formed in the new triangle (either half of the divide) are two 45 degree angles. This is because the two 90 degree angles that have been cut in half are both now 45 degrees, since half of 90 degrees is 45 degrees. The third and last angle is 90 degrees, which is the corner of the former square that had been untouched. These angles fulfill the 180 degree rule for all triangles.
For the side lengths, the two legs of the 45-45-90 triangle are both one, since they were from the sides of the square. If we plug this into the Pythagorean theorem, we see that c, or the hypotenuse, is radical 2. This is because c^2=1+1=2, so we take the radical of it. So, our three side lengths would be, in ascending order, 1, 1, and radical 2. Then, we substitute the values with the variable 'n', where n=1. This shows that these values can be applied to any multiples of themselves. Now the new side lengths would be 'n', 'n', and n radical 2.

Inquiry Activity Reflection
Something I never noticed before about special right triangles is that by using the Pythagorean theorem, we can derive the sides of both of the special right triangles. I can understand how the values came to be in the special right triangles, such as how the 60 degree side of the 30-60-90 triangle was originally radical 3 over 2, until we simplified the sides of the triangle further. It is amazing how the Pythagorean triangle can be applied to so many things!
Being able to derive these patterns myself aids in my learning because if I ever forget the rules of the 45-45-90 or 30-60-90 triangle, I will be able to derive them from the square and the equilateral triangle with the sides lengths of 1. I will know how to use the Pythagorean theorem to determine the sides and then substitute the values for the variable n, so I know that any other multiples of those values can be used. It broadens my understanding of the special right triangles even further because now I have a better grasp of where they come from and what different math concepts could be applied in deriving the special right triangles.

I/D1: Unit N - How do SRT and UC relate?

Inquiry Activity Summary
1. The "30" degree triangle at first has the shortest leg labeled "x", the longer leg labeled "x radical 3", and the hypotenuse labeled as 2x. To simplify the three sides of this triangle so that the hypotenuse=1, I divided all the sides by two. I would then have, in order from shortest to longest side: x/2, (x radical 3)/2, and x. Finally, the last step is to label the ordered pairs. Since the triangle is drawn in the 1st quadrant, all values will be positive. The point at the 30 degrees is the origin, which is (0,0). The point at the 90 degrees, or the square angle, is (radical 3 over 2, 0). This is because we go over (radical 3)/2 units for the x value, while the y value stays the same as 0 since we do not go up or down. Lastly, the point at the 60 degrees will be (radical 3 over 2, 1/2). It has the same x value as the previous ordered pair, but since it goes up 1/2 units, that will become our y value.

2. The "45" degree triangle at first has its two congruent legs labeled as "x", while the hypotenuse is labeled as "x radical 2". To simplify the three sides of this triangle so that the hypotenuse=1, I divided all the sides by radical 2 to cancel out the one on the hypotenuse. I would then have, from the two shortest to the hypotenuse: x/(radical 2), x/(radical 2), and x. Since I cannot have a radical on the bottom of the fraction, I rationalize the two legs by multiplying both the top and bottom of the fraction by radical 2. I would then be left with (x radical 2)/2, (x radical 2)/2, and x. Finally, the last step is to label the ordered pairs. Since the triangle is drawn in the 1st quadrant, all values will be positive. The point at the first 45 degrees is the origin, which is (0,0). The point at the 90 degrees, or the square angle, is (radical 2 over 2, 0). This is because we go over (radical 2)/2 units for the x value, while the y value stays the same as 0 since we do not go up or down. Lastly, the point at the second 45 degrees will be (radical 2 over 2, radical 2 over 2). It has the same x value as the previous ordered pair, but since it goes up (radical 2)/2 units, that will become our y value for this ordered pair.

3. The "60" degree triangle at first has the shortest leg (which is now horizontal) labeled x, the longer leg (which is now vertical) labeled as x radical 3, and the hypotenuse labeled as 2x. To simplify the three sides of this triangle so that the hypotenuse=1, I divided all the sides by 2. I would then have, in order from shortest to longest side: x/2, (x radical 3)/2, and x. Finally, the last step is to label the ordered pairs. Since the triangle is drawn in the 1st quadrant, all values will be positive. The point at the 60 degrees is the origin, which is the ordered pair (0,0). The point at the 90 degrees, or the square angle, is (1/2, 0). This is because we go over 1/2 units for the x value, while the y value stays the same as 0 since we do not go up or down. Lastly, the point at the 30 degrees will be (1/2, radical 3 over 2). It has the same x value as the previous ordered pair, but since it goes up (radical 3)/2 units, that will become our y value.

4. The activity helps derive the unit circle by giving us a much better understanding of it as a whole. We can visualize the special right triangles within the unit circle, realizing that their ordered pairs of the hypotenuse and opposite side will create a part of the circle. We will know where the points had come from, along with their corresponding degrees, due to the special right triangles, and we will realize that the unit circle is entirely made up of those triangles and apply that to our previous knowledge about them.

5. The triangles of this activity lie in the first quadrant, where both x and y are positive. However, the positive values of the ordered pairs will change if you draw them in different quadrants--x will be negative in the second quadrant, y will be negative in the fourth quadrant, and both x and y will be negative in the third quadrant. These will apply to the ordered pairs of the triangles. For example, the 45 degree triangle is drawn in the 2nd quadrant. Therefore, the x of its ordered pair will be negative. The 30 degree triangle is drawn in the 3rd quadrant. Both its x and y will be negative in the ordered pair. Finally, the 60 degree triangle is drawn in the 4th quadrant, so only the y value of the ordered pair is negative.

Inquiry Activity Reflection
The coolest thing I learned from this activity was that all of the special right triangles drawn in the first quadrant of a coordinate plane (starting at the origin) and their reference angles drawn in all the other coordinate planes make up the unit circle! All you have to do is connect the points to form a circle. I understood how to unit circle was formed and now it is easier to memorize it as a whole.
This activity will help me in this unit because I now I have a full understanding of where the unit circle comes from. It helps me in memorizing the unit circle and applying it to later concepts, such as 8 and 9. I know how the ordered pairs on the unit circle were derived and their corresponding degrees as well.
Something I never realized before about special right triangles and the unit circle is that they are both connected! I learned that one can derive the unit circle from special right triangles by using the 45 45 90 and 30 60 90 triangles. I like how trigonometry is built on concepts we studied in geometry. It was really interesting to see how the special right triangles applied to the unit circle and it helped tremendously in memorizing it for me.

RWA1: Unit M Concepts 4-6: Conic Sections in real life

1. Parabola: the set of all points the same distance from a point, known as the focus, and a line, known as the directrix.


2. Description of a parabola: The formula or equation for a parabola is (x-h)^2=4p(y-k) or (y-k)^2=4p(x-h). On a graph, a parabola resembles something similar to a curve, forming an arch-like shape when graphed, and is symmetrical on both sides of its vertex. One of the key features of a parabola is the vertex. It is defined as the point where the parabola crosses its axis, and can be identified using (h,k) of the equation or finding the point that is on the axis of symmetry that "divides" the parabola. Another key feature of the parabola is the aforementioned axis of symmetry. This is the line that the vertex lies on and is what splits the parabola into two symmetrical sides, each mirroring each other. It is either vertical or horizontal, depending on whether the parabola is going up and down or left and right. As a result, the equation of the axis of symmetry will start with x= or y=.

To continue with, there are many other key features to the parabola that are introduced in this unit. One of them is the focus, which lies on the axis of symmetry along with the vertex. The focus will always be "inside" of the parabola, meaning that the parabola will be opening towards it. The closer it is to the vertex, the "skinnier" the graph will be, and the farther away the focus is from the vertex, the "fatter" the graph will be. Since the focus is relatively closer to the vertex, as seen in the picture, the parabola is more skinny that it is fat. The focus point is "p" units away from the vertex, a number that can be determined by referencing the formula of the parabola. The variable "p" can also determine which way the parabola is opening up to--for example if p is positive, the graph will open up or right, while if p is negative, the graph will open down or left. To refer to the picture below once again, the graph is opening right, which tells us that "p" was a positive number. In addition, the same distance p is from the vertex is counted in the opposite direction to determine the directrix, which is a line that is perpendicular to the axis of symmetry.

https://people.richland.edu/james/lecture/m116/conics/translate.html

3. Real World Application: A real world application for the parabola can be seen in the headlights of many automobiles, which are in the shape of paraboloids and help focus light into a certain beam. In other words, the shape of the headlights is concave, allowing more light to be beamed from it. This is because the light is directed to the focus of the parabolic mirror as it travels, then is immediately reflected in straight lines that are parallel to the axis of symmetry. The headlight has a smooth inner surface of a glass reflector, which in turn has a layer of bright aluminum. This part of the object serves as a powerful reflector. As a result, this is what makes the beam of headlights and similar objects to be incredibly strong, projecting light with a wider distance and range. It gives off an intense concentrated beam of light.

The light is also beamed in many directions to encourage safer night driving. Therefore, designers do not want all of the light beams to be parallel to the axis of symmetry--some of the light has to be aimed in different places. To do this, they "offset the filament from the focus and change [the direction of] the beam entirely" (http://www.pleacher.com/mp/mlessons/calculus/appparab.html). The positions that the filaments are in are a major factor in determining the different illumination patters that have been desired. For example, if the filament is directed above the focal point, or the focus, the rays of light will be reflected downward. Similarly, if the filament is directed below the focal point, the rays of light will be reflected upward. And if the filament is positioned behind the focal point, then the rays of light will converge. A video explaining this concept further along with other uses of parabolas in real life is embedded below.

 4. Works Cited:

• http://www.pleacher.com/mp/mlessons/calculus/appparab.html
• http://www3.ul.ie/~rynnet/swconics/UP.htm
• https://people.richland.edu/james/lecture/m116/conics/translate.html